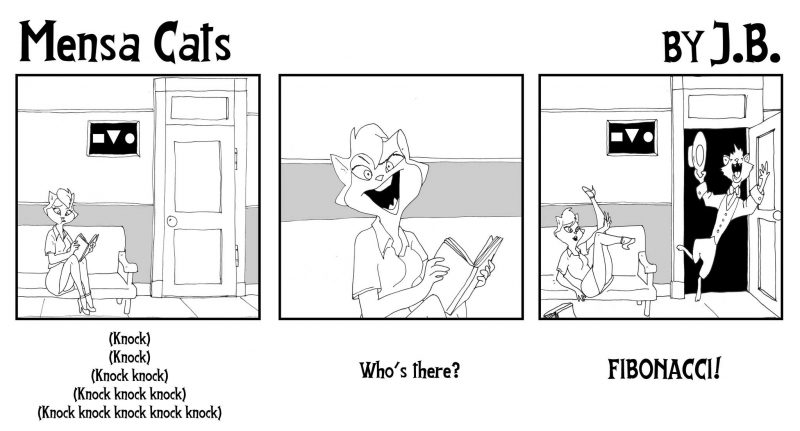
A new mathematical Mensa Cats cartoon by J.B.


We bring you a brand new Mensa Cats cartoon by J.B. (that’s Jason Berry of Vacuum Tree Head). This one expresses not one but two of Zeno’s famous paradoxes in a single frame.
The first is the better-known Dichotomy Paradox, from which the punchline derives. In order to walk into the bar, Zeno (or any of the other patrons) must first walk halfway; and to travel from the halfway point, he must travel half of that distance, and then half of that distance, and so on. It seems that this process of walking halfway would continue forever and one would not arrive and one’s destination, yet we know in reality that we do.
The second paradox is the Arrow Paradox. Consider the frame frozen in time, as indicated by the liquid in mid spill behind the young lady cat, or the multiple instances of Zeno along his path. At any given moment, there is no motion. Zeno’s position does change between moment, but there is an infinite number of other frames, each with a fixed position. As copies/frames of Zeno get closer and closer together, the change in time between them gets infinitesimally small. Yet the process 0f adding up these infinite frames with zero motion in each results in Zeno walking halfway into the bar.
The two paradoxes (and the third, commonly referred to as “Achilles and the tortoise”) are closely related. The first deals with infinitesimal subdivisions of space, while the second deals with infinitesimal subdivisions of time. The key is that while any infinitesimal quantity is smaller than any quantity we can express, it is always still greater than zero. And adding up an infinite number of infinitesimal quantities can sometimes yield a finite number.
Take the halving process in the Dichotomy paradox. Zeno moves half this distance, then half of that, and so on. This can be expressed as an infinite sum.
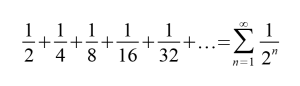
As one gets closer to infinity, the sum gets closer and closer to one. More formally, we can say that as we approach infinity, the sum goes to 1. So an infinite number of subdivisions still reaches our goal of the full distance.
This process of applying operations to an infinite number of infinitesimal subdivisions is the principal behind calculus, and a marvelous thing to behold once one gets used to it. The mathematics does not necessarily answer the metaphysical questions raised by these ancient paradoxes, but it is what most interests us at CatSynth. It’s been a while since we last shared the joy and beauty of mathematics on these pages, but it is high time we resume the practice.
It’s a bit of an on-again-off-again tradition on Pi Day (3-14 in the United States) to share my composition based on the digits of Pi.
It was based on the binary digits rather than decimal digits of Pi, which seemed more universal and also more logical to work with. It uses stretched impulses and square waves for the sounds themselves. At least that is what I recall. It was written in 2011. It’s probably time to revisit the concept with a new piece…
2016 continues to be a year of losses. Below we visit three people whose work has influenced our diverse interests here at CatSynth and who passed away since this holiday weekend.

[By Dontworry (Own work) [CC BY-SA 3.0], via Wikimedia Commons]
Alphonse Mouzon was one of the important early artists in jazz fusion, and performed with many of our musical heroes, including Herbie Hancock, Wayne Shorter, and Gil Evans. In 1971, he joined Wayne Shorter and the rest of Weather Report for their debut album Weather Report. The band has a mixed history – something we should write about on another occasion – but those first albums in the early 1970s have a sound that were quite influential and resonate with those of us who love jazz fusion of that era. You can hear some Mouzon’s 1971 work with Weather Report in this video:
 Vera Rubin is a name that should be better known that it is in popular culture, as her contributions to cosmology and astronomy are central to our current understanding of the universe. Her work made the case for dark matter and its prevalence in the universe. It was another step in the process of understanding our place in the universe. The earth, then the sun, then the galaxy, all became just small and non-centrals parts in a much larger universe; and the discovery of dark matter showed that the “stuff we are made of”, the ordinary baryonic matter (all the chemical elements and such that we learn about in school) is only a small portion of the mass-energy of the universe. Dark matter has since been eclipsed by dark energy in terms of cosmological composition.
Vera Rubin is a name that should be better known that it is in popular culture, as her contributions to cosmology and astronomy are central to our current understanding of the universe. Her work made the case for dark matter and its prevalence in the universe. It was another step in the process of understanding our place in the universe. The earth, then the sun, then the galaxy, all became just small and non-centrals parts in a much larger universe; and the discovery of dark matter showed that the “stuff we are made of”, the ordinary baryonic matter (all the chemical elements and such that we learn about in school) is only a small portion of the mass-energy of the universe. Dark matter has since been eclipsed by dark energy in terms of cosmological composition.
In addition to the grand perspective, Rubin’s work helped us understand why galaxies like our own Milky Way are shaped the way they are and move the way that they do. She was also a strong advocate for women in science, not just in her own career and field but overall in terms of advocacy in inspiration.

[By Riccardo Ghilardi photographer (Own work) [CC BY-SA 3.0 or GFDL], via Wikimedia Commons]
From great science facts we move to great science fiction. Star Wars is one of the important mythologies in contemporary world, and many of us who saw the original movie in 1977 remember it vividly. While Carrie Fisher was not one of the comedic droids or Darth Vader, her character Princess Leia was important to the story in ways a kindergarten-age kid couldn’t quite fathom at the time. What also makes Fisher particularly interesting is how she presented herself, flaws and all, completely outside of the mythology of Star Wars. She was brutally honest and with a dark, dry sense of humor that came out in real life and in Princess Leia. Indeed, after she reprised the role for Episode VII, she was very up front taking on the trolls who mocked for simply doing what we all do: age. Her semi-autobiographical Postcards from the Edge was an accidental discovery in a video store – I liked seeing women leading a dark story, and only afterwords realized that Fisher wrote the screenplay and the original book.
We at CatSynth send our regards to the families of Alphonse Mouzon, Vera Rubon, and Carrie Fisher; and to all those taken by 2016.
It is not uncommon to hear operations on numbers, even the computations carried out in modern computers, as “mere arithmetic.” But arithmetic is hardly simple or obvious when one gets down to the fundamentals and realizes the structure that must be present in our number system in order for it to work they way we intuitively think it should work. Thus, today we consider the Fundamental Theorem of Arithmetic.
Every positive integer (except the number 1) can be represented in exactly one way apart from rearrangement as a product of one or more primes.
Thus every integer has a canonical representation as a product of powers of primes:

where p1 < p2 < … < pk are primes and the αi are positive integers; 1 is represented by the empty product. As example 12 = 22 × 3, and 666 = 2 × 32 × 37. Fairly familiar stuff for anyone who paid attention during grade school and secondary school math classes. But the theorem itself is not self-evident, it is something that had to be proven true in order for our everyday arithmetic to hold. A good article on why the theorem is not obvious can be found here. It also has implications beyond the natural numbers. If we extend the canonical representation to allow both positive and negative values for ai, we get the set of positive rational numbers (fractions), for which the theorem still holds. It can also be generalized to more exotic constructions, such as Gaussian Integers. Gaussian integers, often denoted ℤ[i] are complex numbers a + bi where i is the square root of -1, and a and b are integers. It can be shown that the fundamental theorem of arithmetic holds for Gaussian integers, and that there is a definite set of “Gaussian primes” just as there are prime numbers. But while plotting the prime numbers and looking for visual patterns is an exercise in frustration, the rotational nature of complex numbers (which we have discussed in a previous article) causes the Gaussian primes to fall into a visually interesting radial pattern:

With all the important and sometimes confounding properties of primes, having ways to visualize them is always intriguing.
Any mathematical construct (specifically, a “domain”) that obeys the fundamental theorem of arithmetic is known as a Euclidean Domain. (Note that this has very little to do with Euclidean spaces or the other uses of the term in geometry.) We can observe many more Euclidean domains, such as generalizing Guassian integers to other roots of 1. If we use the cube roots of 1, for example (yes, 1 has three cube roots), we get the set of Eisenstein Integers: numbers of the form a + bω, where a and b are integers and:
![]()
Like Gaussian primes, Eisenstein primes have a distinctive radial pattern when viewed on the complex plane. Whereas Guassian primes divide into quadrants, Eisenstein primes form a hexagonal pattern.

Note that while the generalization works for square roots of -1, cube roots of 1, etc., it doesn’t necessarily work for all roots of 1. Some of those sets will not form Euclidean domains.
We can also look beyond numbers to other mathematical entities that form Euclidean domains. One such example can be found in knot theory, which we discussed in an article a few years ago. Knots can be expressed as unique combinations of prime knots:

From here we can consider the implications for music of the Euclidean domains, the accompanying Euclidean algorithm for computing greatest common divisors in any of these domains. But that will be left as an exercise for another day.