
Graffiti on some ruins in the Sutro Baths. The Cliff House restaurant is visible in the back.
You can see one of our previous photos from this Hipstamatic shoot in a previous Wordless Wednesday.


Graffiti on some ruins in the Sutro Baths. The Cliff House restaurant is visible in the back.
You can see one of our previous photos from this Hipstamatic shoot in a previous Wordless Wednesday.
Today we talk about Lake Merced, as well as the recent video we made featuring it.
Lake Merced is located in the southwestern corner of San Francisco, in the vicinity of the SF Zoo and SF State University.
Despite its odd shape and the fact that it borders three golf courses, it is actually a natural lake. It is fed primarily by an underground spring. In the 19th century, the lake briefly had an outlet to the ocean, approximately where the Great Highway breaks off from Skyline Boulevard, just south of the zoo. The outlet is long gone, but the lake’s ecosystem retains some of its saltwater heritage among the fish and other wildlife that inhabit it. Lake Merced and its surrounding park remain one of the last and largest natural spaces left in the city (in spite of the golf courses), and is home to a variety of plant and animal life. On the day I visited to shoot video, I encountered this egret.
But it is definitely an urban natural space, with sounds and sights from the surrounding city mixing with nature. I am particularly fond of this view looking east over the lake to some apartment buildings. It brings to mind Flushing Meadows in the New York City borough of Queens.
I have been spending more time in the western neighborhoods of San Francisco of late, and Lake Merced is one of the spots I revisit. This is what inspired me to make it the subject of a CatSynth TV video, complete with original synthesizer music.
Here is see the final post-production on the video in Pro Tools. Front and center is Tracktion’s BioTek software synthesizer, which I reviewed during NAMM 2016. It was among the primary instruments used in this video where I blended its mix of natural and traditional-synthesizer sounds with the sounds of the field video.
I also made extensive use of the 4ms Spectral Multiband Resonator and Epoch Modular Benjolin (designed by Rob Hordjik). They both have very elemental sounds that resemble air and water. The Benjolin is chaotic by design, and a small turn of a knob can change it from liquidy to screeching, so it’s sometimes a challenge to get a good recording that fits the concept of the music. The SMR is a lot of fun to play, especially using alternate tunings and changing the spread and morph parameters. A clock is used to constantly shift the bands.
Rounding out the sound palette were the Arturia MiniBrute 2, Mimimoog Model D, and Metasonix R53 vacuum-tube waveshaper and ring modulator.
The Moog Model D, the MiniBrute and several of the modules make cameos during the video, as does Sam Sam. Watch the video all the way through to spot her 😺
This was a fun video to shoot and put together, something a bit more creative and abstract than our usual demos or live-show reports. I have more of these waiting in the queue to be made…
It’s been a busy season for Pitta of the Mind! We had three shows in the span of two months, beginning with our blue set at Pro Arts and culminating with ¡Voltage and Verse! at Adobe Books in San Francisco. You can get a taste for the show in our CatSynth TV video.
It was an honor to once again share a bill with ruth weiss. A Holocaust survivor and founding member of the San Francisco beat poet scene in the 1950s, she is still going strong, performing and supporting local institutions and artists.
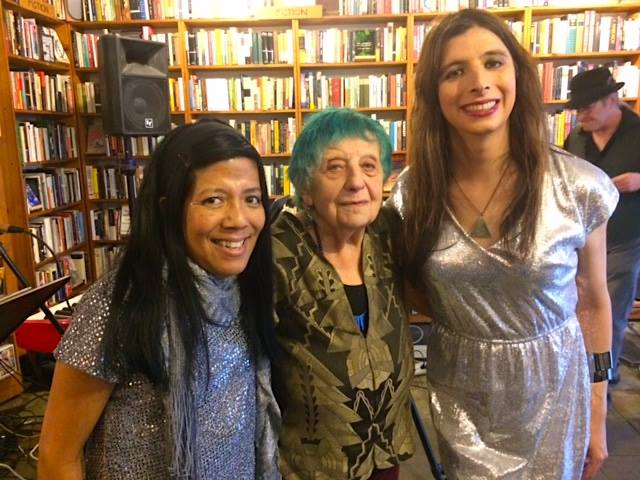
We were glad to see that she is continuing her collaboration with our friend and synthesizer virtuoso Doug Lynner. Together with log percussionist Hal Davis, they performed a set of poetry and music that simultaneously evoked earlier eras and the latest electronic experiments. Davis’ log drum provided an expressive metronome, undulating between a trot and a gallop. Lynner’s synthesizer lines filled in the spaces, sometimes with rhythmic appeggios and at other moments with long eerie drones. The synthesizer timbres and phrases complemented the words in multiple ways, sometimes underpinning the narrative in the manner of a good film score, at other times emphasizing the rhythm of the words and making them into a musical whole.

Our Pitta of the Mind set was part of a month-long celebration for the release of Maw Shein Win’s new book of poetry Invisible Gifts. The book is divided into four sections based on different colors. This works perfectly for our use of color themes in our performances. For this night, we chose silver and performed selections from the silver section of the book. There were some familiar poems that we have performed before, and some that were new to me. There were a variety of styles and subjects in the words that inspired different musical backings, from jazzy electric piano (my favorite) to abstract synthesizer explorations. I was able to reuse some of the modular patches I had developed for my recent show in Portland and make them work with the rhythm of the texts.

Maw and I have performed together so many times now that it has become almost second nature to realize a new set; our three shows this season went off (nearly) flawlessly, and have been among the best we have done in our nearly seven years of collaboration! We have developed a toolset and pallete of instruments (including the Nord Stage and Prophet 12) and sounds that we can quickly turn to with each new text, which makes the process of learning new pieces both simple and fun. I certainly hope we can keep up the momentum in the remainder of the year, even as I turn my own attention to other musical projects.

In between our set and weiss/Lynner/Davis, we were treated to a presentation by Ramon Sender. Sender was a co-founder (along Morton Subotnick and Pauline Oliveros) of the San Francisco Tape Music Center in the early 1960s, but on this evening he regaled us with stories of his time at the Morning Star and Wheeler ranches in Sonoma County in the late 1960s and early 1970s. Morningstar, founded by Lou Gottlieb, was a radical experiment in communal living, populated by an interesting cast of characters along with folks who “commuted” between San Francisco’s Haight-Ashbury district and the ranch west of Sebastopol. It only existed in its communal form for a short period of time before being shut down by Sonoma County. Sender and others then moved to the nearby property of artist Bill Wheeler, who followed Gottlieb’s lead and opened his ranch as a commune open to all. I found myself fascinated by Sender’s stories, and would love to learn more about the history of the area and these communal experiments.
It was a fun night of music and words that lived up to its billing, and I certainly hope to have a chance to perform with everyone again. And thanks to Benjamin Tinker and Adobe Books for hosting the event! Please support your local bookstores and performance spaces.
[Photos not marked “catsynth.com” in this article courtesy of Maw Shein Win.]
The fifth of May marks a great many things. It is the birthday of Karl Marx – indeed, today marks his bicentennial! It is also a day when many Americans inexplicably get drunk and culturally insensitive in celebration of the Mexican defeat of the French Empire in the town of Puebla. And finally, it is National Cartoonists Day. And in honor of this occasion, we celebrate many noted cat cartoonists.
 We begin with B Kilban. An artist originally from Connecticut, he got his start as a cartoonist here in San Francisco, drawing for Playboy. It was at Playboy where his distinctive cat cartoons were discovered by editor Michelle Urry. This led to his most well-known book, Cat. You have probably seen his cats both in formal cartoons and adorning many products. Kilban passed away in 1990, but his legacy lives on through his books and syndication of his images. You can find out more at his official website www.eatmousies.com.
We begin with B Kilban. An artist originally from Connecticut, he got his start as a cartoonist here in San Francisco, drawing for Playboy. It was at Playboy where his distinctive cat cartoons were discovered by editor Michelle Urry. This led to his most well-known book, Cat. You have probably seen his cats both in formal cartoons and adorning many products. Kilban passed away in 1990, but his legacy lives on through his books and syndication of his images. You can find out more at his official website www.eatmousies.com.
 Of course, an article on cat cartoonists must include Jim Davis, the creator of Garfield. Davis grew up on a farm in Indiana with his parents, brother, and 25 cats. While the main human character in Davis’ cartoons, Jon Arbuckle is also a cartoonist who grew up on a farm, the spoiled and overweight Garfield seems nothing like a farm cat. Indeed, his disdain for the concept of catching mice is a frequent topic of the strips. Many an orange male cat has been named “Garfield” in the character’s honor.
Of course, an article on cat cartoonists must include Jim Davis, the creator of Garfield. Davis grew up on a farm in Indiana with his parents, brother, and 25 cats. While the main human character in Davis’ cartoons, Jon Arbuckle is also a cartoonist who grew up on a farm, the spoiled and overweight Garfield seems nothing like a farm cat. Indeed, his disdain for the concept of catching mice is a frequent topic of the strips. Many an orange male cat has been named “Garfield” in the character’s honor.
 One of the best-known works of Japanese manga artist Makoto Kobayashi also features an orange cat. What’s Michael? chronicles the adventures of a shorthair tabby named Michael and his many feline friends. It was originally released in serial form in Japan’s Weekly Morning manga magazine, but it now available in the U.S. as well via Dark Horse Comics. The stories are a mix of the mundane and surreal, with Michael sometimes appearing differently than the orange shorthair title cat, and sometimes even dying in certain episodes.
One of the best-known works of Japanese manga artist Makoto Kobayashi also features an orange cat. What’s Michael? chronicles the adventures of a shorthair tabby named Michael and his many feline friends. It was originally released in serial form in Japan’s Weekly Morning manga magazine, but it now available in the U.S. as well via Dark Horse Comics. The stories are a mix of the mundane and surreal, with Michael sometimes appearing differently than the orange shorthair title cat, and sometimes even dying in certain episodes.
New Yorker cartoonist George Booth is best known his complex doodle-like cartoons featuring befuddled humans and their pets. They are a mainstay of the magazine and synonymous with the “New Yorker style” of cartooning. While the animal most frequently featured in his work is a fat dog with big ears, there are often cats as well.
 And then there is Fritz the Cat, created by the legendary R. Crumb. Fritz originally appeared in Crumb’s homemade comic book “Cat Life”. Originally based on the family cat, Fritz became anthropomorphic in later iterations, evolving into the hedonistic con-artist character that was a mainstay of underground comix in the 1960s. Fritz’s adventures in a New York-like mega-city populated entirely by anthropomorphic animals often devolved into chaos with unusual sexual escapades. In the 1970s, Fritz the Cat was made into an animated feature film by Ralph Bakshi.
And then there is Fritz the Cat, created by the legendary R. Crumb. Fritz originally appeared in Crumb’s homemade comic book “Cat Life”. Originally based on the family cat, Fritz became anthropomorphic in later iterations, evolving into the hedonistic con-artist character that was a mainstay of underground comix in the 1960s. Fritz’s adventures in a New York-like mega-city populated entirely by anthropomorphic animals often devolved into chaos with unusual sexual escapades. In the 1970s, Fritz the Cat was made into an animated feature film by Ralph Bakshi.
 Another underground comix artist Gilbert Shelton created a well-known feline character. Known simply as “Fat Freddy’s Cat”, he initially appeared in Shelton’s Fabulous Furry Freak Brothers strip about a trio of stoner characters in the 1960s before getting his own strip. A standalone series, The Adventures of Fat Freddy’s Cat was published in the 1970s and expanded in a 1980s release.
Another underground comix artist Gilbert Shelton created a well-known feline character. Known simply as “Fat Freddy’s Cat”, he initially appeared in Shelton’s Fabulous Furry Freak Brothers strip about a trio of stoner characters in the 1960s before getting his own strip. A standalone series, The Adventures of Fat Freddy’s Cat was published in the 1970s and expanded in a 1980s release.
 Joann Sfar is a French comics artist. Influenced by the European comics artists of the 20th century including the great Moebius (Jean Giraud), he has a distinctive style that is at once more realistic and fanciful. One of his most well-known series is The Rabbi’s Cat, first released as a comic book in 2005 and later adapted into a film in 2011, which he directed. The main feline character is a cat who has the ability to speak and lives with a rabbi and his daughter in the Jewish community of 1920s Algeria. Sfar’s Jewish heritage runs through many of his works, but no more directly than in The Rabbi’s Cat. In addition to the books, we at CatSynth recommend seeing the film (which is gorgeous) in the original French.
Joann Sfar is a French comics artist. Influenced by the European comics artists of the 20th century including the great Moebius (Jean Giraud), he has a distinctive style that is at once more realistic and fanciful. One of his most well-known series is The Rabbi’s Cat, first released as a comic book in 2005 and later adapted into a film in 2011, which he directed. The main feline character is a cat who has the ability to speak and lives with a rabbi and his daughter in the Jewish community of 1920s Algeria. Sfar’s Jewish heritage runs through many of his works, but no more directly than in The Rabbi’s Cat. In addition to the books, we at CatSynth recommend seeing the film (which is gorgeous) in the original French.
 Another classic of feline cartoons is Krazy Kat, by George Herriman. It had a long run as a comic strip in American newspapers from 1913 to 1944 when Herriman died. The strip was based around the ostensibly simple cat-and-mouse trip, with the cat named Krazy being taunted and tormented by a mouse Ignatz who is often shown throwing bricks at Krazy’s head. Krazy speaks in a very stylized mixture of English and other languages and is of indeterminate gender – though inexplicably smitten with Ignatz.
Another classic of feline cartoons is Krazy Kat, by George Herriman. It had a long run as a comic strip in American newspapers from 1913 to 1944 when Herriman died. The strip was based around the ostensibly simple cat-and-mouse trip, with the cat named Krazy being taunted and tormented by a mouse Ignatz who is often shown throwing bricks at Krazy’s head. Krazy speaks in a very stylized mixture of English and other languages and is of indeterminate gender – though inexplicably smitten with Ignatz.
And finally, we would be remiss if we did not include our very own J.B., author the Mensa Cats series that appears right here on CatSynth.

You can see many more episodes of the Mensa Cats on these pages via this link. We also encourage interested reads to find out more about all the artists discussed in this article and to read their comics.